Wright_Schmidt

Wright Schmidt Telescope

J. A. Hudson

1. The Wright Stuff
2. The Correcting Plate
3. The Primary Mirror
4. The Mounting

1. The Wright Stuff

In the 1930's there was a lot of excitement in the astronomical community over the recent invention by Bernhard Schmidt of the camera that bears his name. The primary mirror was a sphere, and could be made as fast as f:2, or even f:1.5, meaning that only a moderately long exposure could reach very faint stars. The spherical aberration (so named because a sphere cannot render a sharp image of a star, but instead creates a blur) was compensated by a thin plate located at the mirror's center of curvature which was figured to a curve, described by a fourth-order polynomial, which exactly cancelled out the aberration of the primary.

The fact that the Schmidt's entrance pupil, the correcting plate, was located at the center of curvature meant that objects off the central axis would be imaged almost as sharply as they would on center, so the Schmidt was not only a fast camera, but it was wide-field as well, making it a fine instrument for exploring our Milky Way, with its wealth of nebulae, star clusters, and obscuring dust. Moreover, it was an ideal instrument for doing deep-sky surveys, such as the Palomar Sky Survey.

There are several problems with the Schmidt configuration which make it unsuitable for being an amateur's telescope. First, the field of view is strongly curved, meaning that photographic plates had to be bent in order to make use of the wide field. (They would occasionally break!) This could be overcome by means of a field-flattening optic near the focus. Next problem is tube length. If you want a moderately fast Schmidt for visual (as well as photographic) use, you probably want to make the f-number come out to around 4, where ordinary eyepieces can work better. But this means a tube twice as long as the focal length, since the corrector lens has to lie at the mirror's center of curvature (always twice the focal length). Finally, one needs to bring the light out to the side for visual use, so a sizeable secondary mirror is required.

Franklin B.Wright proposed an alternative design, which he described in Amateur Telescope Making, Book Two. Instead of a spherical mirror, his design calls for an oblate sphere, while the curves on the correcting lens are made stronger than in a Schmidt of the same f-number. This results in a flat field, albeit limited by astigmatism to only a couple of degrees of field. But the corrector is located, not at the center of curvature, but at the focus. The more limited field is fine for most eyepieces, and the few Wright telescopes I've read about operate at about f:4.

Fig. 1. Layout of a 9 inch f:4 Wright telescope

The prescription for the above telescope is as follows:

# Wavelengths
lambda     F
lambda     d
lambda     C
# Object Points
object     inf     0.000    0.000
object     inf     0.500    0.000
object     inf     0.750    0.000
# Glasses
Glass      AIR
Glass      523564
# Medium throught object space
medium     AIR
# Surface data
stop       228.60     0.00  1 flat
refr       230.00     9.50  2 polynom  3.03030E-06  -1.53410E-10  -7.62100E-17
refr       230.00   910.70  1 flat
refl       260.00  -911.70  1 polynom -2.73420E-04  -4.03550E-11  -8.04050E-18
screen      50.00     0.00  1 flat

This formula follows exactly the formulae given by Wright in his paper, and this pretty well describes my own Wright telescope. The glass designation 523564 means n_d = 1.523 and V_d = 56.4, the parameters for Pittsburgh Plate Glass "Shadowgraph Crown." The units are in mm. for linear dimensions; angles are expressed in degrees. For each surface, the type of surface is followed by its diameter (assumed round), distance to next surface, index in the table of glasses (AIR=1 here), and the shape of the surface. The polynomial surfaces give the coefficients for r², r⁴, and r⁶. The following are ray-trace results:

Fig. 2. Wavefront aberrations of the f:4 Wright telescope

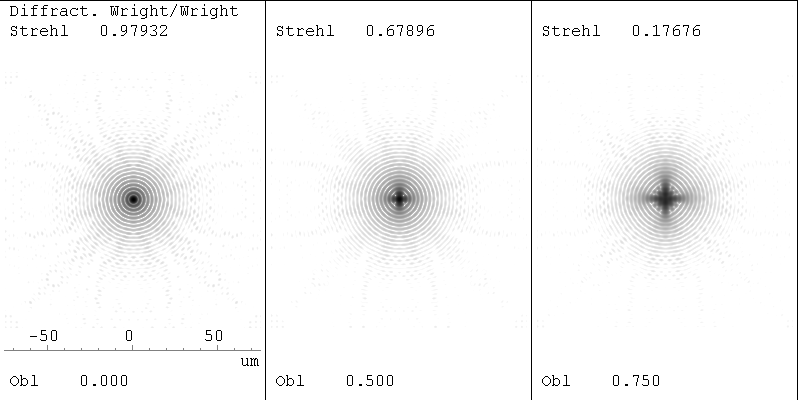
Fig. 3. Diffraction images for the f:4 Wright telescope

Note that astigmatism is the limiting aberration for off-axis images. (This is true also for the Schmidt; however, these only become a problem at much larger field angles.) So we see the Wright f:4 is good out to about 1/2 degree, and certainly acceptable photographically at 3/4 degree and even beyond.

Wright's original equations are these:
s = -(F-M) r² / [2(n-1)EF] + M r⁴ / [16(n-1)EF³] + (4E+F)M r⁶ / [192(n-1)E²F⁵],
x = [E-(F-M)] y² / (4EM) + [M-(F-M)] y⁴ / (32EM ³) + (E+M)M y⁶ / (384E²M⁵),
F-M = (3k²/64)[1 + 0.08k²]F,
k = D/F.
Here, s is the deviation of the lens surface from flat; likewise x is the deviation of the mirror's surface from flat. F is the focal length, D the diameter of the corrector (so the f number is F/D), M the distance between center of mirror and focus, E the separation of lens from mirror, and r and y both stand for radial distances from the centers.Wright's sign convention is exactly opposite to that chosen by the software for the prescription above, but I wanted to present his equations exactly as published.

The configuration I've described is my own 9 inch Wright. It is a delight to use with a wide-field Erfle eyepiece. Photographically it works well, too, although I've thus far not invested in a camera that can accomodate the full field.

Fig. 4. M101 taken with Atik 16 HR with 9 inch Wright

My friend, Bob Bolster, and I both undertook the making of Wright telescopes. His was a 12 inch, and mine a 10 inch, which I found worked much better at a 9 inch aperture, avoiding vignetting and not an altogether perfect job of fabricating the optics. I think Bob's 12 inch turned out somewhat better.

Fig. 5. M42 taken by Ken Short, using Bob Bolster's 12 inch Wright at Hopewell Observatory

2. The Correcting Plate

Of course, how to go about making these strongly aspheric surfaces? Bob and I set about the following strategy: We would first finish my 10 inch primary mirror to as good a sphere as we could. Setting this up for testing at its center of curvature, we then placed each of the correctors in front of the sphere, and measured zones, much as you would figuring a paraboloidal mirror.

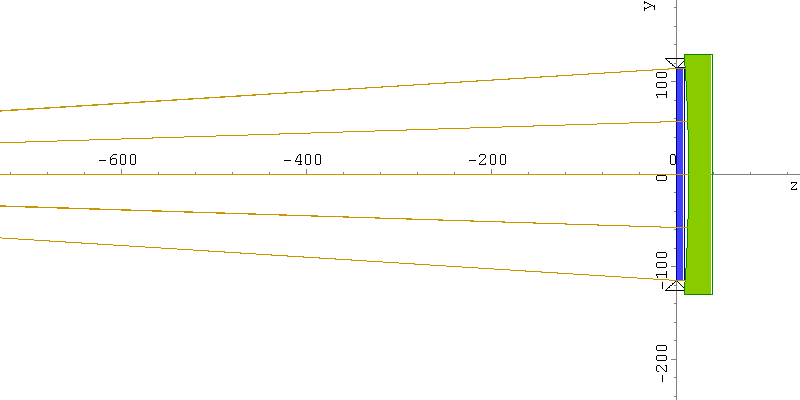
Fig. 6. Layout for testing correcting plate against spherical mirror.

The longitudinal aberration plot for this setup is shown here:

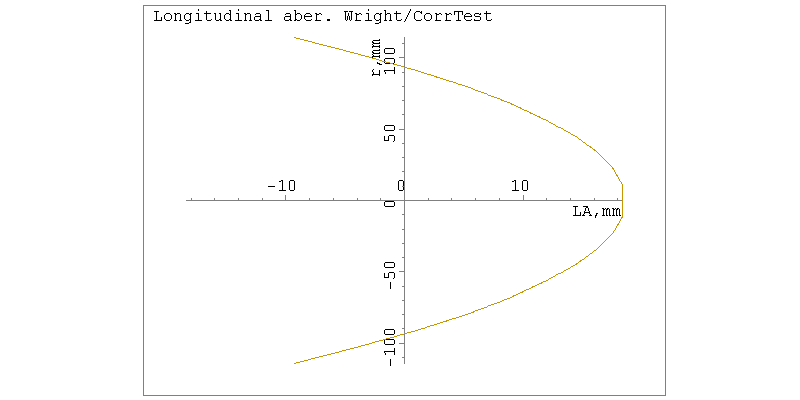
Fig. 7. Longitudinal aberration for corrector in front of spherical mirror

The prescription for this ray-trace is as follows:

# Wavelengths
lambda     d
# Object Points
object     -1818.700    0.000    0.000
# Glasses
Glass       AIR
Glass       523654
# Medium throughout object space
medium     AIR
# Surface data
stop       228.60     0.00   1 flat
refr       230.00     9.50   2 polynom     3.03030E-06  -1.53410E-10  -7.62100E-17 
refr       230.00     4.00   1 flat
refl       260.00    -4.00   1 sphere     -1830.0000
refr       230.00    -9.50   2 flat
refr       230.00 -1818.7    1 polynom     3.03030E-06  -1.53410E-10  -7.62100E-17 
screen      50.00     0.00   1 flat

The common convention followed here is that light rays move from negative to positive coordinates, the z axis being chosen as the optical axis. Thus, the object point is situated at z =-1818.7 mm. The stop is at the lens, since it limits the bundle of rays coming in. Next is the front surface of the correcting plate, whose equation is given in the form z = a₂ r² + a₄ r⁴ + a₆ r⁶. The coefficients are such that the value of z comes out in millimeters. The sphere is the test sphere of radius 1830 mm. Note here that the convention for calculating the LA (Longitudinal Aberration) follows the same sign convention. Thus, rays coming back from the lens under test at increasing radial distance from the center are focused farther and farther toward -z, meaning back towards the observer whose eyepoint is near the object point. And so, the appearance of the lens under the Foucault test is just like that of a hyperbolic mirror, with about 4 times the correction as that of a parabolic mirror at f:4. In our test setup, knife edge and slit moved together, and the z distance was read off a dial guage (with large travel). The center to edge zone readings were about 30 mm apart. Each zone, once you get past the blur at the middle, is pretty sharply defined. A rule with pins in it is laid across the lens, and where the border between light and dark crosses the rule defines the zone radius, r, for any setting of the knife edge.

But how to get to this stage of correction? Bob and I took two very different paths. I polished my lens first to a plano-convex sphere, the radius chosen from the sag of the 6th-order curve minus the sag at the edge. The sag of this curve was only 0.013 mm or about 0.0005 inch - barely measurable with a precision Starret dial guage. The maximum deviation of the 6th order curve desired and this sphere amounted to only about 7 microns, and I resolved to figure the curve entirely by local polishing. Bob, on the other hand, thought it better to grind in some of the correction using tiles on a flexible backing. In retrospect, I think Bob was right to do this--his corrector was much more free of zones than mine. Measurements made during grinding were done with the same Starrett dial guage mounted on a jig with pointed legs so the guage measured the sag at the point of greatest deviation.

A disk supported all around its edges will deform, under uniform loading, to a shape that is described by a 4th order polynomial in the radial coordinate (see, for instance, Roark). If a thin correcting plate is loaded uniformly by exposing one side to a vacuum, a deflection can be found for which its deformation is just right for grinding the exposed side either flat of to a shallow sphere. This sphere can then be tested by interference for figuring, and when the pressure is equalized, the plate assumes the correct Schmidt form. Bernard Schmidt used exactly this technique in producing the world's first Schmidt camera.

We first tried the vacuum method for forming the correctors. Bob had made an aluminum casting with a thick flange, with a large O ring set in it, and we had a go at bending his 12 inch corrector blank. This technique is described by others (e.g. Bob May), so I won't go into it here except to say it was a failure for us because our vacuum wouldn't hold. You see, it was a dumb thing to use a casting. Only proper way to make the chamber is out of a solid, thick piece of plate steel or aluminum. Castings are porous! We did learn an interesting fact: the partial vacuum needed is only perhaps a third of an atmosphere below ambient; your lungs are capable of sucking this amount of air out of the chamber--you don't need a pump! A dial gauge is used to determine when the correct deformation has taken place, and the valve closed.

A final thought I had is inspired by hearing that Celestron makes their correctors by the Schmidt method; however the plate is sucked down into conformity with a carefully machined surface to assure exactly the desired deformation. The advantage here is obvious: careful regulation of the pressure is unnecessary so long as the back of the lens blank is in contact with the plate. It occurs to me that perhaps it isn't necessary to provide a very exactly-machined back plate. If center and edge are of the correct difference, the overall deflection should be correct, and the unsupported parts of the lens don't matter any more than they would if there were no back plate, unless the pressure difference were so excessive that high-order zones are produced. In other words, the pressure regulation requirement is re-instated in part, but not so stringently as for the totally unsupported lens.

Is the sixth-order really necessary? At least in small apertures like these, and at f:4, no. I stuck to the 6th order curves as specified by Wright, but a good corrector can be made by going no farther than fourth order.

3. The Primary Mirror

This proved to be every bit the challenge that the correcting lens was. The difference between a sphere of radius 1829mm (72 inches) and the Wright curve amounts to 5.4 X 10^-3 mm, very nearly equal in size to the difference between a parabola of the same radius; however, of opposite sign. In other words, one tries to create an "up edge" on the mirror for the Wright, as opposed to a down edge for the parabola. The knife-edge position, instead of -r²/2R (knife and slit move together), it is r²/2R. One must move the knife edge inward in increasing amounts as you go from the center zone to the edge.

Both Bob and I figured the Wright curve starting from a sphere, using local polishers. Again, Bob proved himself the master optician by showing a smooth curve, whereas mine was zony. I calculated the zones to be within 1/8 wave tolerance, but nevertheless, they show up if I put a knife edge on a star. The aperture grays over uniformly, except for little ridges and valleys, somewhat along the lines of Everest's "Apologies to Unk" in ATM Two, "Unk" being "Unk" Ingalls, the editor. Nevertheless, star images appear sharp, and I've split double stars down to 1", not quite to Dawes' limit. For photos, the telescope works well. Bob's is even better, as the denizens of Hopewell Observatory will tell you.

There are a couple of approaches that can be taken that avoid zone-to-zone testing. One is to construct a null lens optic which compensates for the Longitudinal Aberration (LA) seen at the center of curvature for the Wright primary. Another, more innovative, one is described by Prof. Everhart. Sad to say, his paper is behind a paywall, but I'll try to describe it here. The Wright primary is very nearly an oblate sphere, with its flattened center and curled-up edges.

Everhart throws away the r⁶ term for the mirror, quite justified at f:4. His equation for the primary mirror is given as:
w = r²/(4F) + r⁴/(32cF⁴)
where c = E/F. Usually c is chosen to be about 1.05 to give room for (in those days) a film holder. w takes the place of Wright's x, and r replaces y. This equation can be put in the form
(w-cF)² / (c²F²) + r² / (2cF²) = 1,
again omitting higher-order terms in r, which is justified. Here we indeed have the equation of an ellipse, or, rotating it about its axis of symmetry, we obtain an oblate sphere.

An ellipse, as we all learn in school, has two foci, and in the above equation, their separation is 2 (2c-c²)^1/2 F. Since c is close to 1, we see that the separation is roughly 2F, or the radius of the primary. The semi-minor axis of the ellipse is cF, so if we were to locate the slit (but not a long slit) a distance cF behind the mirror under test, and (2c - c²)^1/2 F to the side, with the knife edge an equal distance on the opposite side, we should be able to get a null cut-off. There is the complication that, since the axis of symmetry doesn't run along a line between source and knife-edge, one must mask off all but a strip of the mirror in the plane of this ellipse.

Everhart completed his telescope in 1980 for his private observatory; after his death, it was donated to the Guffey Charter School in Denver. Professor Everhart had been the director of the Chamberlain Observatory at the University of Denver. Bob and I were privileged to meet him one summer when he visited Stellafane. At that same session, if I recall correctly, we met Tom Waineo, from Space Optical Systems, who was also constructing a Wright telescope. We lost track of the fate of that instrument. (Hopefully, I'll get some comments on that.)

4. The Mounting

The tube in which you put your optics deserves some attention.

Bob was taking no chances: He built a Serrurier truss using aluminum plate at the junctions and Invar for the struts. A no-nonsense approach, and it worked out well. However, it might be instructive to recount my many mistakes, hoping others will profit, or maybe get a laugh or two.

I, instead, thought the telescope should have a tube, and made one out of fiberglass cloth, wrapped around a cardboard tube, using epoxy for the cement. Epoxy is exothermic, and how! In quantities I was using, it got very hot to the touch. Naturally, the hotter it gets, the faster it sets. One should use it in smaller doses. This isn't possible for a good-sized tube, so the other option is to coat the fiberglass with a light coat made from a small batch, let it set, and then coat again. Also, use the woven cloth (somewhat more expensive), not the blanket type, as I did. After the mess hardened, there were hours spent in smoothing with a belt sander, and little scruffs of the fiber still were visible. A coat of epoxy paint hid these mistakes, and it ended up a success, so I thought. My wife asked, "What's that? A hot water heater?"

For a while, the 9 inch rode as a passenger on an astrographic mount. This mounting uses an extended polar axle with a bearing box at its end; a shaft running through the box for the declination axis carries saddle plates on both sides. Thus, two telescopes can be mounted, and moved together. The lighter one of course needs some extra weights to maintain balance. I took some successful eclipse pictures this way, while Bob took some also with his 12 inch Wright. We proved that two Wrights don't make a wrong.

Bob made several worm wheels using his lathe, an indexing head, and a special hob he crafted and fired up to harden the teeth. He kindly gave one of these, 12 inches in diameter, to me for my own mounting. I constructed a German mount which carried both my 9 inch Wright and a 6 inch Schiefspiegler. I tilted its primary morror with little calibrated screws in order to search for a bright guide star. I mounted a Nikon camera back at the Newtonian focus of the Wright. By this time, I had moved to Charlottesville, VA, and enjoyed a dark sky at our home at Shadwell. Of the many photos attempted, only a few didn't show excess trailing. The fiberglass was not stiff enough, and there was no doubt some deforming of the Schiefspiegler box in which its optics resided.

Finally, I took Bob's example to heart and made a Serrurier truss. I used galvanized steel tubing rather than Invar, the price being important. This tube doesn't sag! I experimented with a pickoff mirror and separate eyepiece mount for guiding; the mirror could be rotated to sample different parts of the field until a sufficiently bright star was found. Later I dispensed with guiding altogether, prefering to take short CCD exposures and stack them.

Here is how the telescope is now mounted.

Fig. 8. 9 inch Wright showing truss tube, camera holder with filter wheel, and eyepiece where CCD camera is placed.

The truss is visible at top and bottom; on the camera side the struts are separated enough to make room for the focuser and for camera, filter wheel, etc. The mount is now a fork. The camera is used unguided at present. The telescope is located in a roll-off roof structure; a gate to the south opens up, allowing the roof to move over the telescope, which has to be placed in a horizontal stow position. Two worm gears provide for the motions; they are cut from HDPE plastic. The declination wheel was cut by a tap and the plastic held in a jig to let the tap advance the blank as the threads were cut. Naturally, they don't come out to a whole number of teeth; the discontinuity is hidden where the telescope doesn't go. For the polar worm, I used the jig shown below to gash the teeth.

Fig. 9. Gashing the polar worm wheel using a small circular saw with hand-filed cutter Chicago 12 in. worm wheel used to index.

The gashing was indexed using a 12 inch worm gear with 96 teeth. I wanted 120 teeth in the 16 inch blank, and so had to turn the worm 0.8 turn for each tooth. The shape of the cutter was made to match the commercial (Chicago Gear Works) 8-pitch gear. I had to hand-cut and file the cutting teeth. (It didn't chatter too badly!) The cutter has to be tilted slightly to match the worm. I simply bought an 8-pitch Chicago worm to use in the telescope. After the gear was mounted on the telescope, and the gear box was in place, I attached a 1/2 inch power drill to the shaft extension, and drove the gear (not clamped to the telescope!) while directing a heat gun to the worm. This works nicely. Be careful to allow this to run several minutes after removing the heat.

References